"Decimal" .NET Type vs. "Float" and "Double" C/C++ Type
Posted by gregd1024 on December 10, 2007
Have you ever wondered what is the difference between the .NET “Decimal” data type and the familiar “float” or “double”? Ever wonder when you should one versus the other? In order to answer these questions, take a look at the following C# code:
using System; using System.Collections.Generic; using System.Linq; using System.Text; namespace IEEE_Floating_Point_Problems { class Program { static void Main(string[] args) { int iteration_num = 1; Console.WriteLine("First loop, using float type:"); // runs only four times instead of the expected five! for(float d = 1.1f; d <= 1.5f; d += 0.1f) { Console.WriteLine("Iteration #: {0}, float value: {1}", iteration_num++, d.ToString("e10")); } Console.WriteLine("\r\nSecond loop, using Decimal type:"); // reset iteration count iteration_num = 1; // runs correctly for five iterations for(Decimal d = 1.1m; d <= 1.5m; d += 0.1m) { Console.WriteLine("Iteration #: {0}, Decimal value: {1}", iteration_num++, d.ToString("e10")); } Console.WriteLine("Press any key to continue..."); Console.ReadKey(); } } }
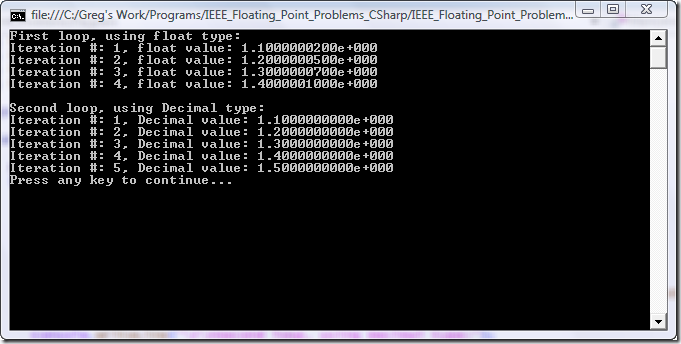
Here is what the output looks like:
At first glance, looking at the code and not the output, it seems like the first for() loop should run for five iterations. After all, there are five values from 1.1 up to and including 1.5 stepping by 0.1 (i.e. 1.1, 1.2, 1.3, 1.4, and 1.5). But in reality, the loop only runs through four iterations. Why is this? Also, why was 1.10000002 assigned as the first value of “d” instead of the hard-coded 1.1? The reason is simple – we’re working on hardware that uses binary floating point representation as opposed to decimal representation. Binary floating point is really an approximation of the true decimal number because it is base two (binary) instead of base 10 (decimal).
In order to understand this better, we’ll take the common (IEEE 754) floating point formula but use base 10 instead of two:
Filling in the variables to represent a value of 1.1 we get:
+1 * (1 + 0.1) * 10^0 =
(1 + 0.1) * 10^0 =
1.1 * 10^0 =
1.1 * 1 = 1.1 <— Exactly the correct value
In the real base two version everything is the same except 10 changes to a two:
If you try to fill in this equation, you’ll immediately see the problem when converting 0.1 (the fraction part) into binary. Let’s do it here:
-
0.1 x 2 = 0.2; so the binary digit is 0
-
0.2 x 2 = 0.4; so the binary digit is 0
-
0.4 x 2 = 0.8; so the binary digit is 0
-
0.8 x 2 = 1.6; so the binary digit is 1
-
0.6 x 2 = 1.2; so the binary digit is 1
-
0.2 x 2 = 0.4; so the binary digit is 0
-
0.4 x 2 = 0.8; so the binary digit is 0
-
0.8 x 2 = 1.6; so the binary digit is 1
-
0.6 x 2 = 1.2; so the binary digit is 1
-
0.2 x 2 = 0.4; so the binary digit is 0
-
0.4 x 2 = 0.8; so the binary digit is 0
-
0.8 x 2 = 1.6; so the binary digit is 1
-
0.6 x 2 = 1.2; so the binary digit is 1
-
and so on…
We end up with “0001100110011…” where the four digits at the end (0011) repeat forever. Therefore, it’s impossible to represent 0.1 with an exact binary number. If we can’t represent 0.1 exactly, then the rest of the equation will not evaluate precisely to 1.1; rather, it will be slightly more or slightly less depending on how many bits of precision you have available. This explains why the hard-coded “1.1” value changed slightly once assigned to the “d” variable. It can never be exactly 1.1 because the hardware is incapable of representing it.
These small precision errors get compounded in the first loop as 0.1 is added to “d” after each iteration. By the fifth time around “d” is slightly greater than 1.5 causing the loop to exit (the value of 1.5 can be represented exactly in binary and is not approximated). Therefore only four iterations are run instead of the expected five.
The .NET Decimal Type
So what’s the deal with this .NET “Decimal” type? It is simply a floating point type that is represented internally as base 10 instead of base two. Obviously with base 10 (our real-world numbering system) any decimal number can be constructed to the exact value without approximating. This is why the second for() loop runs for the expected five iterations and the variable “d” always has the exact hard-coded value assigned to it.
The Decimal type is really a struct (in C# and MC++) that contains overloaded functions for all math and comparison operations. In other words, it’s really a software implementation of base 10 arithmetic.
Which Type Should I Use?
Since Decimal types are perfectly accurate and float’s are not, why would we still want to use the intrinsic float/double types? Short answer – performance. In my speed tests Decimal types ran over 20 times slower than their float counterparts.
So if you’re writing a financial application for a bank that has to be 100% accurate and performance is not a consideration, use the Decimal type. On the other hand, if you need performance and extremely small floating point variations don’t affect your program, stick with the float and double types.
Other Considerations
Another thing the Decimal type can do that the float and double types cannot is encode trailing zero’s (note: there are some base two architectures, non-Intel, that can encode trailing zero’s – but those are out of the scope of this article). For example, there is a difference between 7.5 and 7.50 in the Decimal type, but there is no way to represent this in a standard float/double. Let’s look at another example – check out the following MC++ code:
#include "stdafx.h" #include <stdio.h> using namespace System; int main(array<System::String ^> ^args) { double number = 1.23+1.27; Console::WriteLine("double: {0}", number); Decimal decimal = (Decimal)1.23+(Decimal)1.27; Console::WriteLine("decimal: {0}", decimal); Console::WriteLine("Press any key to continue..."); Console::ReadKey(); return 0; }
The first part that uses a double outputs 2.5, but the second one that uses a Decimal outputs 2.50 – we didn’t even have to specify a format string in order to get that trailing zero. This could be very useful in applications that deal with dollar amounts.
More Information
If you want to get more information regarding binary floating point versus decimal floating point, see this awesome FAQ by IBM:
Conclusion
I hope this has shed some light on the differences between the .NET Decimal type and the standard float/double types. If you have any questions or notice any typos in this article, please email me through my Contact page:
https://gregs-blog.com/contact
Thanks for reading! 🙂
-Greg Dolley
Kaeli’s Space » Blog Archive » .NET Decimal vs. float / double - What’s the Difference? said
[…] “Decimal” .NET Type vs. “Float” and “Double” C/C++ Type Share and Enjoy: These icons link to social bookmarking sites where readers can share and discover new web pages. […]
Suketu said
Very useful article. Thanks..
One question..Is it the same difference for T-SQL float and decimal data-types?
gregd1024 said
Suketu – I *think* so, but can’t say with absolute certainty. Try checking the doc’s and look at the data-type’s range – if it has a base of 2 raised to some power, then it’s binary decimal; if it’s 10 raised to some power then it’s real decimal.
-Greg
Batman said
Thanks for the article, I found it to be very helpful.
gregd1024 said
Batman – glad you liked it! 🙂
-Greg
ianthe said
Greg,
Thanks so much for this article. This helped me in resolving some discrepancies in my financial computations.
gregd1024 said
Ianthe – Awesome! I’m glad it helped! 😉
-Greg
Kanu Gami said
Thanks.
Its very helpful article.
– Kanu Gami
Mahdi said
Thanks.
Really helped ….
Mahdi
Santosh said
very informative article, thanks.
Yae said
Thank you for this post, it save me a lot of time, I was lost breaking my head without logical explanation, because results wasn’t the expected since I was using float when what I need to use Decimal. Thank you….
Adam Nofsinger said
Hey, thanks for this good explanation. Makes sense.
BTW, as of 2008-05-23, you are #1 on google for keywords “C# float vs decimal vs double”.
🙂
gregd1024 said
Hey, I am #1. Nice! 🙂
JIV said
Thank you,
an engineering type of answer,it is getting into the core of the problem, which makes easilly to remember.
justice said
i’m greateful to ur elaborating
Luba said
Great article and examples. This clarified my doubts. Thanks!
jhons said
thank you. 🙂
jhons said
what about the the difference of float from double in c programming language?
gregd1024 said
Jhons – the difference between float and double in C is simply the data type size. They both hold floating point numbers, but “float” is 4 bytes (32 bit) and “double” is 8 bytes (64 bit) on most C compilers.
-Greg Dolley
MK said
Thanks so much for the article.
gregd1024 said
MK – you’re welcome! 😉
Manish Buhecha said
Wow, great work and good explanation…
Thanks
Dennis said
Since I just had an argument with a college about double having 15 digits behind the decimal point so what do you need more for precision here another factor in favor for decimal:
Even thought double has 15 digits after the digital point, double do not save x digits in front of the decimal point and 15 behind but it converts each number to 0.xxxxx having 15 digits behind and only a zero in front of the point.
Or in a more specific example 123.456 is saved internally as 0.123456e+003
This results into the following behavior:
using System; namespace ConsoleApplication1 { class Program { static void Main(string[] args) { Console.WriteLine("Decimal value with quite a few digits:"); decimal x = 12345678901234567890.1234567890m; Console.WriteLine("decimal: {0}", x.ToString("N10")); int j; for (j = 0; j < 100000; j++) x += 1.0m; Console.WriteLine("decimal: {0} ...", x.ToString("N10")); Console.WriteLine(" ... after Incrementing {0:N} times", j); Console.WriteLine("Same with double:"); double y = 12345678901234567890.1234567890d; Console.WriteLine("double: {0}", y.ToString("N10")); for (j=0 ; j < 100000; j++) y+= 1.0; Console.WriteLine("double: {0} ...", y.ToString("N10")); Console.WriteLine(" ... after Incrementing {0:N} times", j); } } }So as a resume as long as you need less than 15 digits in common you still have a choice about decimal or double based on the thoughts above, but starting at 15 digits you need to take decimal as well.
But also decimal has its limits so with 29 digits it ends as well!
gregd1024 said
Dennis – very nice example and thanks for the info! For everyone else that just wants to see the output without building the project, here ya go:
——————- Output ——————————————
Decimal value with quite a few digits:
decimal: 12,345,678,901,234,567,890.1234567890
decimal: 12,345,678,901,234,667,890.1234567890 …
… after Incrementing 100,000.00 times
Same with double:
double: 12,345,678,901,234,600,000.0000000000
double: 12,345,678,901,234,600,000.0000000000 …
… after Incrementing 100,000.00 times
—————– End Output ——————————————
-Greg Dolley
Hua-Jun Zeng said
Very good article!
Keith said
Hi, great article!
I have a set of classes where I need to compile them to use float, double or decimals depending on the target. Any ideas on how to easily swap all float references for doubles for example to compile two different targets?
Using something like “class MYNumber : Double” so that it is only necessary to change one line of code does not work as Double is sealed, and obviously there is no #define in C#, so I am at a loss on how to do this apparently simple task!
Thanks.
Keith said
Answer to this question here
gregd1024 said
Keith – a while back I was thinking about how to do this; at first, I thought just to make a wrapper class around all the possible data types, but your link has a simpler solution (in the comment on Aug 26,16:21). Thanks for the link. 🙂
Saurabh Vats said
Thanks a lot greg for this useful article very informative
Eric Braun said
Excellent. Saved me a long debugging session to find sum differences! Thank you.
gregd1024 said
Eric – nice! NP.
hurf said
“Binary floating point is really an approximation of the true decimal number because it is base two (binary) instead of base 10 (decimal).”
There are an infinite number of ways to represent numbers in binary format. Among these, an infinite number of them allow a number exactly equal to .1 to be represented. And, an infinite number fail to exactly represent .1. The standard format for floating point numbers in binary fails to represent .1, but not because it’s binary.
An object in computer memory, such as a .NET Decimal, will also fail to accurately represent some numbers, even if they are decimal–if not because its format explicitly limits the number of digits it can represent, as with a Float, then because it’s stored in a physical device, and to represent some numbers it would need more memory than the device possessed. Such a number, whose exact representation in some given decimal format would occupy many gigabytes, is unlikely to arise in banking… but it does exist.
Also, decimal numbers are not “our real-world numbering system”. The fact that humans happen to have ten fingers doesn’t magically make one numbering system more real than others.
You’re talking about a few specific, practical matters in a way that makes them sound mathematically universal.
Floating Point Math « Kaizen – Continuous Improvement said
[…] Floating Point Math Posted on July 19, 2010 by Manjunath Bhat Made simple […]
Ivan said
Thank you. This was written in a way, so I even understood it 🙂 I just loved the example with base 2 vs base 10. Thanx a bunch
ShariqShariq said
> So if you’re writing a financial application for a bank that has to be 100% accurate and performance is not a consideration, use the Decimal type.
What does 100% accurate mean? To determine accuracy, you must also determine the precision. For example, if I divide 100 by 3 and state that the answer must be precise to the nearest integer (perhaps because my processor only supports this level of precision) then the answer is 33 and that’s 100% accurate.
However, if I specify my precision to 3dp, then the answer is 33.333 (again, 100% accurate).
A decimal type in C# has a precision of 28-29 significant figures (http://msdn.microsoft.com/en-us/library/364x0z75.aspx). The “actual” answer for 100/3 is 33 and an infinite number of 3’s after the decimal point. The decimal type will truncate this to 25-26 3’s. That’s not the actual answer, it’s an answer that’s 100% accurate to 25-26 decimal places.
So…
Go ahead and use doubles (ie floating point numbers) and convert to decimal at the end. Just don’t try comparing variables of type double with each other or you’ll enter a world of pain.